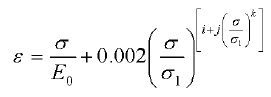In molte applicazioni nel campo delle connessioni elettriche per il settore automotive, sia per simulare il processo produttivo di stampaggio, sia per considerare l’insieme delle sollecitazioni in esercizio, è necessario analizzare il comportamento dei materiali metallici in campo non lineare.
La nostra esperienza ci ha portato a considerare inadeguato l’utilizzo del modello bi-lineare (BISO - Bilinear Isotropic Hardening), in quanto, pur avendo il vantaggio di richiedere unicamente la conoscenza dei valori di tensione e di deformazione nei punti di snervamento e di rottura, non permette di ottenere una corretta stima delle deformazioni plastiche, almeno nel caso delle leghe metalliche utilizzate nelle nostre applicazioni. L’esigenza di utilizzare modelli multi-lineari, come il MISO (Multilinear Isotropic Hardening), anche in assenza di una completa caratterizzazione del materiale, ci ha portato a cercare una semplice metodologia, che permettesse di approssimare l’andamento della curva σ-ε in tutto campo di esistenza, partendo dalla conoscenza dei soli valori di carico e deformazione nei punti di snervamento e di rottura.
Alla base di questa metodologia abbiamo posto l’utilizzo dei metodi di fitting “full-range” per materiali metallici. L’utilizzo di questi semplici metodi, congiunto con quello del modello MISO, ci ha permesso di ottenere una corretta stima del comportamento in ambito plastico nella maggior parte dei casi analizzati. Il modello MISO, utilizzato per le nostre analisi in ambito termo-strutturale, utilizza come input i valori di sforzo e deformazione, ottenuti con il metodo “full-range” proposto da MacDonald nel 2000 come rielaborazione di quanto presentato da Ramberg e Osgood nel loro Report NACA del giugno 1943. Il modello matematico, messo a punto da MacDonald, sfrutta le stesse informazioni che si utilizzerebbero per implementare un modello bi-lineare, con l’introduzione di tre coefficienti aggiuntivi i, j e k, determinati sulla base di dati sperimentali. I coefficienti, compresi in un range tra 2.5 e 6, sono principalmente funzione, a parità di materiale, della geometria dell’applicazione. Di seguito si riporta la formulazione algebrica proposta da MacDonald, con i tre coefficienti cui si è accennato.
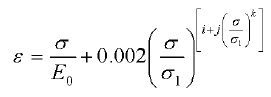
Negli ultimi anni sono stati sviluppati altri metodi full-range, solitamente caratterizzati da formulazioni di maggiore complessità. Questi metodi solitamente suddividono la formulazione algebrica della curva σ-ε in due tratti separati, uno per la parte lineare (σ≤σ0.2 ) ed uno per quella non lineare. Il miglioramento nell’approssimazione della curva ottenibile non compensa, a nostro avviso, la maggiore complicazione, spesso legata ad un incremento del numero di coefficienti introdotti. |